Kinematic Lab Mov permite la medida de determinados parámetros cinemáticos angulares durante movimientos habituales para su posterior evaluación en un contexto clínico, readaptativo o de rendimiento. Ver tutorial
¿Qué es Kinematic Lab Mov?
Aunque el movimiento humano se realiza siempre mediante combinaciones de distintos tipos de desplazamientos articulares (deslizamientos y rotaciones en varios planos), nuestros movimientos articulares son esencialmente movimientos angulares. Es decir, un segmento rota sobre un eje articular y describe un ángulo. Estos movimientos reciben distintos nombres en función de los planos en los que se realizan: por ejemplo: flexión y extensión si se re- alizan en un plano sagital o abducción y aducción si se realizan sobre el plano frontal.
Gracias a la longitud de los segmentos óseos y a estos desplazamientos angulares los movimientos humanos gozan de la amplitud adecuada para interactuar y adaptarse adecuadamente en entornos cambiantes. Permitiendo, por ejemplo una buena amplitud de zancada en la marcha o la carrera y un rango de alcance o empuje óptimo en los miembros superiores.
Ya que nuestros movimientos son esencialmente angu- lares, parece lógico poder cuantificar ciertos parámetros cinemáticos sobre los mismos. Especialmente en contex- tos clínicos o de readaptación. Para poder evaluar las car- acterísticas de este tipo de movimientos necesitamos re- currir a la cinemática angular.
La cinemática describe parámetros importantes de los movimientos en relación al tiempo, por ejemplo la velocidad y la posición en instantes concretos, así como las causas que los originan o modifican durante su transcurso. La aplicación Kinematic LabMov permite la medida de determinados parámetros cinemáticos angulares durante movimientos habituales para su posterior evaluación en un contexto clínico, readaptativo o de rendimiento. Los movimientos que permite analizar kinematic LabMov se han agrupado por regiones anatómicas y por tipos de movimiento articular para poder ser empleados como test de evaluación muscular de los parámetros en diferentes momentos del tiempo, por ejemplo, podemos evaluar una abducción de hombro en un sujeto cuando inicia la recu- peración e ir evaluando el movimiento semanalmente, comparando valores de amplitud (ROM) y potencia del movi- miento. En cualquier caso, es muy importante que la grabación del gesto se realice perpendicularmente al plano por el que transcurre el mismo.
¿Cómo funciona Kinematic Lab Mov?
Para la realización de los cálculos oportunos, necesitamos conocer algunas variables del movimiento. Kinematic Lab Mov obtiene estas variables iniciales a partir de una grabación en video desde tu smarthphone. En el mercado existen diferentes wearables, es decir, dispositivos que lleva el propio usuario (generalmente puls- eras, o elementos fijados mediante cintas a los segmentos corporales) y que registran a determinadas frecuencias distintos parámetros del movimiento mediante acelerómetros, magnetómetros y osciloscopios. Estas medidas son enviadas a un teléfono móvil, tablet o pc y allí son procesadas y presentadas como tablas de datos, gráficos, etc…
La opción de obtener los datos cinemáticos mediante una grabación de video tiene como ventaja su simplicidad y su bajo coste. En determinados contextos, resulta más cómodo grabar un simple video de un movimiento del sujeto que estar colocando sensores durante minutos. Así mismo, estos wearables no están al alcance de todos las personas por sus costes (que oscilan entre los 250 € y los 6000 €) en función de sus diferentes prestaciones. Con la app Kinematic Lab Mov sólo necesitas grabar un vídeo del movimiento y seleccionar sobre éste una serie de intervalos que permitirán al algoritmo realizar los cálculos necesarios.
¿Cómo calcula Kinematic Lab Mov?
Los parámetros cinéticos básicos son el espacio y el tiempo durante el cuál se desarrolla un movimiento. Ambos obtenidos a través de la adquisición de vídeo. Una vez grabado el vídeo, nuestra app accede al sistema operativo del smarthphone y nos proporciona un sistema de coordenadas sobre el propio vídeo que nos permite marcar una serie de puntos de referencia espaciales y medir sus instantes temporales.
Ya hemos dicho que en el cuerpo humano los movimiento son esencialmente angulares, por lo que el primer punto que debemos definir es el eje de rotación (0,0) sobre el que rota el segmento cuyo movimiento estamos analizando. Ese será nuestro principal punto de referencia para el cálculo. Una vez definido el punto sobre el cual rota el segmento el siguiente dato de interés es la longitud del mismo. La longitud del segmento que se desplaza corresponde con una medida que se obtienen de manera automática por la aplicación a partir de la talla del sujeto en relación a tablas que ofrecen valores relativos de segmentos en relación a la estatura. Con la referencia de rotación marcada y la longitud del segmento el usuario debe marcar puntos en el extremo del segmento que se moviliza a lo largo de la trayectoria que describe el movimiento en cuestión. El primer punto a marcar es el que corresponde con el instante de inicio del movimiento, a partir de este, podrá marcar tantos puntos como desee. Cuantos más puntos se marquen, más valores se obtienen y más precisa es la valoración cinemática. Cada punto que marcamos en la trayectoria del movimiento Kinematic LabMOV define un intervalo espacial en un determinado tiempo que permite obtener un valor de la velocidad angular (ω) en ese intervalo concreto. El valor del tiempo transcurrido entre intervalos se obtiene a través de los fotogramas de vídeo entre dos puntos marcados consecutivamente en la trayectoria del movimiento; de manera que el valor de tiempo (t) a partir de un número de fotogramas puede obtenerse según la expresión.
t =
1 frecgr
⋅ nºfotogramas
de esta manera por ejemplo si grabamos a la mayor frecuencia que permite el iPhone 6 (240 fps) y han transcurrido 20 fotogramas entre dos puntos marcados, el valor en segundos sería:
t =
1 240
⋅ 20 = 0,08 s
El ángulo recorrido () por el segmento que corresponde con el espacio se obtienen mediante vectores trazados sobre el espacio virtual de coordenadas a partir del punto fijado como eje de rotación. De esta manera disponemos de posición angular en el instante de tiempo preciso y podemos calcular el valor de velocidad angular en ese punto:
ω =
t
(en rad ⋅ s-1)
La velocidad promedio de cada uno de los intervalos marcados se puede obtener a partir de los incrementos de (t), de manera que los valores promedio de velocidad angular en cada intervalo marcado se obtienen según;
ω =
Δ Δt
; para intervalos concretos, ω1 =
1 – i t1 – ti
….ωn =
n – n-1 tn – tn-1
Una vez obtenida la velocidad angular para cada intervalo, podemos obtener la aceleración angular α(t) para cada de manera que,
α =
Δω Δt
(en rad ⋅ s-2)
y se pueden obtener valores de la tasa de cambio de velocidad entre los diferentes intervalos marcados:
ω =
ω1 – ωi t1 – ti
; α2 =
ω2 – ω1 t2 – t1
….αn =
ωn – ωn-1 tn – tn-1
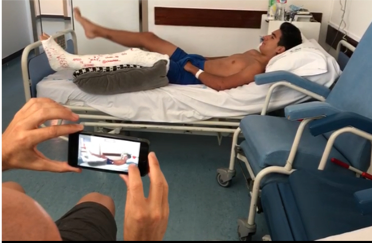
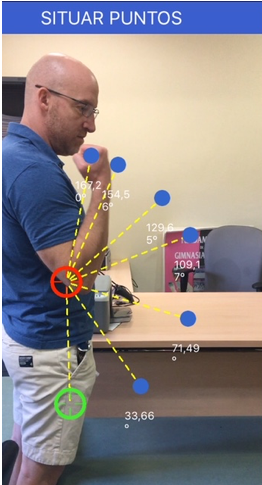
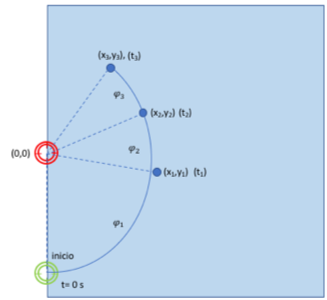
De esta forma el usuario marca puntos de interés en la trayectoria del movimiento y Kinematic LabMov obtiene valores de velocidad angular y aceleración para cada intervalo. Los valores de aceleración permiten la obtención de variables dinámicas, como son el torque o momento de la fuerza (M) y la obtención del valor de potencia. Para las estimaciones de torque o momento del movimiento es necesario recurrir a la 2ª Ley de Newton para rotación que se expresa como:
∑ i
Mi = I ⋅ α
Donde I representa el momento de inercia del sistema (que para una masa puntual se expresa como I = m⋅r2) y describe la forma en la que la distribución de la masa del mismo influye en su tendencia a girar, y α es la aceleración angular (que se obtuvo anteriormente a partir de la tasa de cambio de ω(t). El valor I de puede calcularse considerando que el movimiento angular articular presenta un momento de inercia correspondiente al de una masa puntual sujeta al extremo de una varilla que rota sobre su otro extremo, pudiendo expresarse como:
I = m1 ⋅ r2 +
1 3
m2 ⋅ r2 = (m1 +
1 3
m2 ) r2
En un movimiento corporal los momentos de inercia (M) que producen rotación son tres y de manera general el momento resultante se expresa como una suma de todos ellos:
Momento que genera la carga externa ⟹ M1 = -m1 ⋅ g ⋅ r ⋅ sen
Siendo m1 la carga externa; r la longitud del segmento que se desplaza (introducida por el usuario de la app) y el valor del ángulo en el instante del movimiento marcado por el usuario
Momento que genera el propio segmento ⟹ M2 = -m2 ⋅ g ⋅
r 2
⋅ sen
Siendo m2 la masa relativa del segmento corporal que se desplaza; r/2 el punto aproximado en el que se localiza el centro de masa del segmento que se desplaza y el valor del ángulo en el instante del movimiento marcado por el usuario
Momento que generala fuerza muscular ⟹ MF = -F ⋅
r 3
⋅ sen30º = F ⋅
r 6
Siendo F la fuerza generada por la musculatura agonista; r/2 es una aproximación de la inserción muscular relativa a la longitud del segmento que se desplaza y sen 30 = 1/2 el valor aproximado del ángulo con el que el tendón ejerce la fuerza de tracción sobre el segmento corporal. Hasta este punto disponemos de los siguientes datos conocidos:
- m1 es la carga externa que se añade al movimiento y se selecciona en el panel de opciones en caso de realizar el movimiento con una mancuerna u otro medio de carga (en kg).
- m2 es la masa del segmento o segmentos corporales que se desplazan y se obtiene mediante datos obtenidos de tablas que proporcionan el peso relativo de los diferentes segmentos en relación al peso corporal del sujeto. La app obtiene este valor a partir del peso del sujeto que se aporta como dato por el operador.
- r y fracciones de son la medida del segmento que se moviliza y se obtiene a partir de la estatura del sujeto. Las fracciones de corresponden a localizaciones de centros de masas o puntos de tracción relativas a la longitud del segmento.
- ángulo es el valor angular de la posición del segmento en cada instante que el usuario marca como punto de referencia del movimiento.
- El momento de inercia I del sistema (m1 + 1/3 ⋅ m2)⋅r2
- El valor de la aceleración angular (α) que se obtienen considerando la tasa de cambio de ω(t) ⟹ α = Δω/Δt
El único valor no conocido es el valor del momento de la fuerza muscular F que puede obtenerse despejando de la siguiente ecuación:
∑ i
Mi = I ⋅ α
⟹ MF = -F ⋅ [-m1 ⋅ g ⋅ r ⋅ sen – m2 ⋅ g ⋅
r 2
⋅ sen ] + F ⋅
r 6
= ( m1 +
1 3
m2 ) r2 ⋅ α
Simplificando los términos y despejando nuestra incógnita, F nos queda:
F = (6m1 + 3m2) ⋅ g ⋅ sen + (6m1 + 2m2) ⋅ r ⋅ α
La ecuación anterior aproxima los valores de fuerza muscular a partir de los datos proporcionados y obtenidos a partir de los cálculos anteriores. Obsérvese la coherencia entre las dependencias del valor de la fuerza muscular, con cada una de las masas implicadas (especialmente la carga externa, m1), la longitud del segmento (r), el ángulo (), el valor de la aceleración angular (α) y la influencia de g. De esta forma, aportando el valor de (), cada vez que se marca un punto en la app y mediante la ecuación anterior se aproxima el valor de la fuerza muscular F, en ese punto. Como cada valor de (), se registra junto a un valor de velocidad angular (ω) , podemos obtener el valor de potencia P en ese punto considerando que la potencia , puede expresarse como el producto de la fuerza por la velocidad, o en este caso, del momento de la fuerza muscular M por la velocidad angular (ω) :
P = M ⋅ ω (en W)